A tiež zvážte dôležitú praktickú aplikáciu témy: štúdium systému lineárnych rovníc pre kompatibilitu.
Aká je hodnosť matice?
Vtipný epigraf článku obsahuje veľa pravdy. Samotné slovo „rank“ sa zvyčajne spája s nejakou hierarchiou, najčastejšie s kariérnym rebríčkom. Čím viac vedomostí, skúseností, schopností, spojení atď., má človek. - čím vyššia je jeho pozícia a rozsah príležitostí. Z hľadiska mladosti sa hodnosť vzťahuje na celkový stupeň „tvrdosti“.
A naši matematickí bratia žijú podľa rovnakých princípov. Zoberme si na prechádzku niekoľko ľubovoľných nulové matice:
Zamyslime sa, či v matici iba nuly, tak o akej hodnosti môžeme hovoriť? Každý pozná neformálny výraz „úplná nula“. V matrixovej spoločnosti je všetko úplne rovnaké:
Poradie nulovej maticeakákoľvek veľkosť je nula.
Poznámka : nulová matica je označená gréckym písmenom "theta"
Pre lepšie pochopenie poradia matice budem ďalej čerpať z materiálov analytická geometria. Zvážte nulu vektor nášho trojrozmerného priestoru, ktorý neudáva určitý smer a je na budovanie zbytočný afinný základ. Z algebraického hľadiska sú súradnice daného vektora zapísané v matice„jeden po troch“ a logické (v špecifikovanom geometrickom zmysle) predpokladajme, že hodnost tejto matice je nulová.
Teraz sa pozrime na niekoľko nenulové stĺpcové vektory a riadkové vektory:
Každá inštancia má aspoň jeden nenulový prvok, a to je niečo!
Poradie ľubovoľného nenulového riadkového vektora (stĺpcového vektora) sa rovná jednej
A všeobecne povedané - ak je v matici ľubovoľné veľkosti má aspoň jeden nenulový prvok, potom jeho poradie nie menej Jednotky.
Algebraické riadkové vektory a stĺpcové vektory sú do určitej miery abstraktné, preto sa opäť obraciame ku geometrickej asociácii. nenulová vektor udáva presne definovaný smer v priestore a je vhodný na konštrukciu základ, takže hodnosť matice sa bude považovať za rovnú jednej.
Teoretické pozadie : v lineárnej algebre je vektor prvkom vektorového priestoru (definovaného 8 axiómami), ktorým môže byť najmä usporiadaný riadok (alebo stĺpec) reálnych čísel s operáciami sčítania a násobenia reálnym číslom definovaným pre nich. Viac informácií o vektoroch nájdete v článku Lineárne transformácie.
lineárne závislé(vyjadrené cez seba). Z geometrického hľadiska obsahuje druhý riadok súradnice kolineárneho vektora 
, ktorá vec v stavebníctve neposunula dopredu trojrozmerný základ, ktoré sú v tomto zmysle nadbytočné. Hodnosť tejto matice sa teda tiež rovná jednej.
Súradnice vektorov prepíšeme do stĺpcov ( transponovať maticu):
Čo sa zmenilo z hľadiska hodnosti? Nič. Stĺpce sú proporcionálne, čo znamená, že poradie sa rovná jednej. Mimochodom, všimnite si, že všetky tri riadky sú tiež proporcionálne. Môžu byť identifikované podľa súradníc tri kolineárne vektory roviny, z toho len jeden užitočné pre konštrukciu "plochého" základu. A to je v úplnom súlade s naším geometrickým zmyslom pre hodnosť.
Z vyššie uvedeného príkladu vyplýva dôležité tvrdenie:
Poradie matice podľa riadkov sa rovná poradiu matice podľa stĺpcov. Už som to trochu spomenul v lekcii o efektívnosti metódy na výpočet determinantu.
Poznámka : lineárna závislosť riadkov vedie k lineárnej závislosti stĺpcov (a naopak). Ale aby som ušetril čas a zo zvyku, takmer vždy budem hovoriť o lineárnej závislosti strún.
Pokračujme vo výcviku nášho milovaného maznáčika. Pridajte súradnice ďalšieho kolineárneho vektora do matice v treťom riadku 
:
Pomohol nám pri budovaní trojrozmerného základu? Samozrejme, že nie. Všetky tri vektory kráčajú tam a späť po rovnakej ceste a poradie matice je v poriadku. Môžete vziať toľko kolineárnych vektorov, koľko chcete, povedzme 100, umiestniť ich súradnice do matice 100 x 3 a poradie takého mrakodrapu zostane stále jedna.
Zoznámime sa s maticou, ktorej riadky lineárne nezávislé. Dvojica nekolineárnych vektorov je vhodná na konštrukciu trojrozmernej bázy. Hodnosť tejto matice je dva.
Aká je hodnosť matice? Čiary sa nezdajú byť proporcionálne ... takže teoreticky tri. Hodnosť tejto matice sa však tiež rovná dvom. Pridal som prvé dva riadky a dolu som zapísal výsledok, t.j. lineárne vyjadrené tretí riadok cez prvé dva. Geometricky riadky matice zodpovedajú súradniciam troch koplanárne vektory, a medzi touto trojicou je dvojica nekolineárnych súdruhov.
Ako môžeš vidieť lineárna závislosť v uvažovanej matrici nie je zrejmé a dnes sa len naučíme, ako ju priviesť „do čistej vody“.
Myslím, že veľa ľudí háda, aká je hodnosť matice!
Uvažujme maticu, ktorej riadky lineárne nezávislé. Vytvoria sa vektory afinný základ a hodnosť tejto matice je tri.
Ako viete, každý štvrtý, piaty, desiaty vektor trojrozmerného priestoru bude lineárne vyjadrený pomocou základných vektorov. Ak sa teda do matice pridá ľubovoľný počet riadkov, potom jej poradie budú ešte tri.
Podobné uvažovanie je možné vykonať pre matice väčších veľkostí (jasne, už bez geometrického významu).
Definícia : poradie matice je maximálny počet lineárne nezávislých riadkov. alebo: poradie matice je maximálny počet lineárne nezávislých stĺpcov. Áno, vždy sa zhodujú.
Z vyššie uvedeného vyplýva dôležitý praktický návod: poradie matice nepresahuje jej minimálny rozmer. Napríklad v matici 
štyri riadky a päť stĺpcov. Minimálny rozmer je štyri, preto poradie tejto matice určite nepresiahne 4.
Notový zápis: vo svetovej teórii a praxi neexistuje všeobecne uznávaný štandard na označovanie hodnosti matice, najbežnejší možno nájsť: - ako sa hovorí, Angličan píše jedno, Nemec druhé. Preto na základe známej anekdoty o americkom a ruskom pekle označme hodnosť matice rodným slovom. Napríklad: . A ak je matica „bezmenná“, ktorých je veľa, môžete jednoducho napísať.
Ako nájsť hodnosť matice pomocou maloletých?
Ak by naša babička mala v matici piaty stĺpec, mal by sa vypočítať ďalší moll 4. rádu („modrá“, „malina“ + 5. stĺpec).
Záver: maximálne poradie nenulového molla je tri, takže .
Možno nie každý úplne pochopil túto frázu: maloletý 4. rádu sa rovná nule, ale medzi maloletými 3. rádu bola nenulová jednotka - teda maximálne poradie nenulové vedľajší a rovný trom.
Vynára sa otázka, prečo rovno nevypočítať determinant? Po prvé, vo väčšine úloh matica nie je štvorcová a po druhé, aj keď získate nenulovú hodnotu, úloha bude s vysokou pravdepodobnosťou zamietnutá, pretože zvyčajne znamená štandardné riešenie zdola nahor. A v uvažovanom príklade nám nulový determinant 4. rádu dokonca umožňuje tvrdiť, že poradie matice je len menšie ako štyri.
Musím sa priznať, že na analyzovaný problém som prišiel sám, aby som lepšie vysvetlil spôsob ohraničovania maloletých. V reálnej praxi je všetko jednoduchšie:
Príklad 2
Nájdite hodnosť matice metódou fringingu maloletých 
Riešenie a odpoveď na konci hodiny.
Kedy funguje algoritmus najrýchlejšie? Vráťme sa k rovnakej matici štyri krát štyri 
. Je zrejmé, že riešenie bude najkratšie v prípade „dobrého“ rohových maloletých: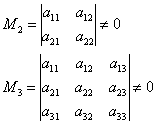
A ak , potom , inak - .
Myslenie nie je vôbec hypotetické – existuje veľa príkladov, kde sa celá vec obmedzuje len na uhlových maloletých.
V niektorých prípadoch je však efektívnejšia a vhodnejšia iná metóda:
Ako nájsť poradie matice pomocou Gaussovej metódy?
Táto časť je určená čitateľom, ktorí už poznajú Gaussova metóda a postupne sa im to dostalo do rúk.
Z technického hľadiska táto metóda nie je nová:
1) pomocou elementárnych transformácií privedieme maticu do stupňovitého tvaru;
2) poradie matice sa rovná počtu riadkov.
To je úplne jasné pomocou Gaussovej metódy sa nemení poradie matice a podstata je tu mimoriadne jednoduchá: podľa algoritmu sa v priebehu elementárnych transformácií zistia a odstránia všetky nepotrebné proporcionálne (lineárne závislé) čiary, v dôsledku čoho zostáva „suchý zvyšok“ - maximálny počet lineárne nezávislé čiary.
Transformujme starú známu maticu súradnicami troch kolineárnych vektorov: 
(1) Prvý riadok bol pridaný k druhému riadku, vynásobený -2. Prvý riadok bol pridaný k tretiemu riadku.
(2) Nulové čiary sú odstránené.
Zostáva teda jeden riadok, teda . Netreba dodávať, že je to oveľa rýchlejšie ako vypočítať deväť nulových maloletých 2. rádu a až potom vyvodiť záver.
Pripomínam vám to samo o sebe algebraická matica nič sa nedá zmeniť a transformácie sa vykonávajú len za účelom zistenia hodnosti! Mimochodom, opäť sa pozastavme nad otázkou, prečo nie? Zdrojová matica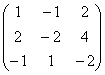 
nesie informáciu, ktorá sa zásadne líši od maticovej a riadkovej informácie. V niektorých matematických modeloch (bez preháňania) môže byť rozdiel v jednom čísle otázkou života a smrti. ... Spomenul som si na školských učiteľov matematiky základných a stredných ročníkov, ktorí nemilosrdne ukrátili známku o 1-2 body za najmenšiu nepresnosť alebo odchýlku od algoritmu. A bolo to hrozné sklamanie, keď namiesto zdanlivo zaručenej „päťky“ to dopadlo „dobre“ alebo ešte horšie. Pochopenie prišlo oveľa neskôr – ako inak zveriť človeku satelity, jadrové hlavice a elektrárne? Ale nebojte sa, v týchto oblastiach nepracujem =)
Prejdime k zmysluplnejším úlohám, kde sa okrem iného zoznámime s dôležitými výpočtovými technikami Gaussova metóda:
Príklad 3
Nájdite hodnosť matice pomocou elementárnych transformácií 
Riešenie: vzhľadom na maticu štyri krát päť, čo znamená, že jej poradie určite nie je vyššie ako 4.
V prvom stĺpci nie je žiadna 1 alebo -1, preto sú potrebné ďalšie kroky na získanie aspoň jednej jednotky. Počas celej existencie stránky som opakovane dostával otázku: „Je možné zmeniť usporiadanie stĺpcov počas elementárnych transformácií? Tu - preusporiadaný prvý alebo druhý stĺpec a všetko je v poriadku! Vo väčšine úloh kde Gaussova metóda, stĺpce sa naozaj dajú preusporiadať. ALE NIE. A nejde ani o prípadnú zámenu s premennými, ide o to, že v klasickom kurze vyučovania vyššej matematiky sa s týmto úkonom tradične nepočíta, preto sa na takéto ukrivenie bude pozerať VEĽMI krivo (alebo dokonca nútené všetko prerobiť) .
Druhý bod sa týka čísel. Pri rozhodovaní je užitočné riadiť sa nasledujúcim všeobecným pravidlom: elementárne transformácie by mali, ak je to možné, znížiť čísla matice. V skutočnosti je oveľa jednoduchšie pracovať s jedna-dva-trojka ako napríklad s 23, 45 a 97. A prvá akcia nie je zameraná len na získanie jednotky v prvom stĺpci, ale aj na elimináciu čísel 7 a 11.
Najprv úplné riešenie, potom komentáre: 
(1) Prvý riadok bol pridaný k druhému riadku, vynásobený -2. Prvý riadok bol pridaný k tretiemu riadku, vynásobený -3. A do kopy: k 4. riadku pribudol 1. riadok vynásobený -1.
(2) Posledné tri riadky sú proporcionálne. Vymazaný 3. a 4. riadok, druhý riadok bol presunutý na prvé miesto.
(3) Prvý riadok bol pridaný k druhému riadku, vynásobený -3.
Matica zmenšená do stupňovitého tvaru má dva riadky.
Odpoveď:
Teraz je rad na vás, aby ste mučili matricu štyri na štyri:
Príklad 4
Nájdite hodnosť matice pomocou Gaussovej metódy 
Pripomínam ti to Gaussova metóda neznamená jednoznačnú rigiditu a vaše riešenie sa s najväčšou pravdepodobnosťou bude líšiť od môjho riešenia. Krátka ukážka úlohy na konci hodiny.
Akú metódu použiť na zistenie poradia matice?
V praxi sa často vôbec nehovorí, akou metódou treba hodnosť nájsť. V takejto situácii je potrebné analyzovať podmienku - pre niektoré matice je racionálnejšie vykonať riešenie prostredníctvom maloletých, zatiaľ čo pre iné je oveľa výhodnejšie použiť elementárne transformácie:
Príklad 5
Nájdite hodnosť matice 
Riešenie: prvý spôsob akosi hneď zmizne =)
O niečo vyššie som odporučil nedotýkať sa stĺpcov matice, ale keď existuje nulový stĺpec alebo proporcionálne / zodpovedajúce stĺpce, stále stojí za to amputovať: 
(1) Piaty stĺpec je nula, odstránime ho z matice. Hodnosť matice je teda najviac štyri. Prvý riadok sa vynásobí -1. Toto je ďalšia charakteristická vlastnosť Gaussovej metódy, vďaka ktorej je nasledujúca akcia príjemnou prechádzkou:
(2) Ku všetkým riadkom, počnúc druhým, bol pridaný prvý riadok.
(3) Prvý riadok sa vynásobí -1, tretí riadok sa vydelí 2, štvrtý riadok sa vydelí 3. Druhý riadok vynásobený -1 sa pripočíta k piatemu riadku.
(4) Tretí riadok bol pridaný k piatemu riadku, vynásobený -2.
(5) Posledné dva riadky sú proporcionálne, piaty vypúšťame.
Výsledkom sú 4 riadky.
Odpoveď:
Štandardná päťposchodová budova pre sebaobjavovanie:
Príklad 6
Nájdite hodnosť matice
Krátke riešenie a odpoveď na konci hodiny.
Treba si uvedomiť, že slovné spojenie „matrix rank“ nie je v praxi až také bežné a vo väčšine problémov sa bez neho zaobídete. Existuje však jedna úloha, v ktorej je hlavnou postavou posudzovaný koncept, a na záver článku zvážime túto praktickú aplikáciu:
Ako skúmať kompatibilitu systému lineárnych rovníc?
Často popri riešení sústavy lineárnych rovníc podľa podmienky je najprv potrebné preskúmať jej kompatibilitu, teda dokázať, že nejaké riešenie vôbec existuje. Kľúčovú úlohu pri tomto overovaní zohráva Kronecker-Capelliho veta, ktorý sformulujem v požadovanom tvare:
Ak hodnosť systémové matice rovná hodnosti systém rozšírenej matrice, potom je systém konzistentný a ak sa dané číslo zhoduje s počtom neznámych, potom je riešenie jedinečné.
Preto, aby sme študovali kompatibilitu systému, je potrebné skontrolovať rovnosť 
, kde - systémová matica(zapamätajte si terminológiu z lekcie Gaussova metóda), a - systém rozšírenej matrice(t.j. matica s koeficientmi pri premenných + stĺpec voľných členov).
Na prácu s pojmom hodnosť matice potrebujeme informácie z témy "Algebraické doplnky a vedľajšie. Druhy vedľajších a algebraických doplnkov" . V prvom rade ide o pojem „matrix minor“, keďže hodnosť matice určíme práve cez maloletých.
Hodnosť matice vymenovať maximálne poradie jeho maloletých, medzi ktorými je aspoň jeden, ktorý sa nerovná nule.
Ekvivalentné matice sú matice, ktorých poradie je si navzájom rovné.
Poďme si to vysvetliť podrobnejšie. Predpokladajme, že medzi maloletými druhého poriadku je aspoň jeden iný ako nula. A všetci maloletí, ktorých poradie je vyššie ako dva, sa rovnajú nule. Záver: poradie matice je 2. Alebo napríklad medzi maloletými desiateho rádu je aspoň jeden, ktorý sa nerovná nule. A všetci maloletí, ktorých poradie je vyššie ako 10, sa rovnajú nule. Záver: poradie matice je 10.
Hodnosť matice $A$ je označená nasledovne: $\rang A$ alebo $r(A)$. Hodnosť nulovej matice $O$ je nastavená na nulu, $\rang O=0$. Pripomínam, že na vytvorenie matice minor je potrebné prečiarknuť riadky a stĺpce, ale nie je možné prečiarknuť viac riadkov a stĺpcov, ako obsahuje samotná matica. Napríklad, ak matica $F$ má veľkosť $5\krát 4$ (t.j. obsahuje 5 riadkov a 4 stĺpce), potom maximálne poradie jej vedľajších prvkov je štyri. Už nebude možné vytvárať neplnoleté deti piateho rádu, pretože budú vyžadovať 5 stĺpcov (a my máme len 4). To znamená, že poradie matice $F$ nemôže byť väčšie ako štyri, t.j. $\rang F≤4$.
Vo všeobecnejšej forme vyššie uvedené znamená, že ak matica obsahuje $m$ riadkov a $n$ stĺpcov, potom jej poradie nemôže presiahnuť najmenšie z čísel $m$ a $n$, t.j. $\rang A≤\min(m,n)$.
V zásade spôsob jej zisťovania vyplýva zo samotnej definície hodnosti. Proces hľadania poradia matice podľa definície možno schematicky znázorniť takto:
Dovoľte mi vysvetliť tento diagram podrobnejšie. Začnime uvažovať úplne od začiatku, t.j. s maloletými prvého poriadku nejakej matrice $A$.
- Ak sú všetky neplnoleté osoby prvého rádu (to znamená prvky matice $A$) rovné nule, potom $\rang A=0$. Ak medzi maloletými prvého poriadku je aspoň jeden, ktorý sa nerovná nule, potom $\rang A≥ 1$. Prechádzame k overovaniu maloletých osôb druhého rádu.
- Ak sa všetci maloletí druhého poriadku rovnajú nule, potom $\rang A=1$. Ak medzi maloletými druhého rádu je aspoň jeden, ktorý sa nerovná nule, potom $\rang A≥ 2$. Prechádzame k overovaniu maloletých tretieho rádu.
- Ak sú všetky neplnoleté osoby tretieho rádu rovné nule, potom $\rang A=2$. Ak je medzi maloletými tretieho rádu aspoň jeden, ktorý sa nerovná nule, potom $\rang A≥ 3$. Prejdime ku kontrole maloletých štvrtého rádu.
- Ak sú všetky neplnoleté osoby štvrtého rádu rovné nule, potom $\rang A=3$. Ak existuje aspoň jeden nenulový menší stupeň štvrtého rádu, potom $\rang A≥ 4$. Prechádzame k overovaniu maloletých piateho rádu atď.
Čo nás čaká na konci tejto procedúry? Je možné, že medzi maloletými k-tého rádu je aspoň jeden, ktorý sa líši od nuly, a všetci maloletí (k + 1)-ého rádu sa budú rovnať nule. To znamená, že k je maximálne poradie maloletých, medzi ktorými je aspoň jeden, ktorý sa nerovná nule, t.j. poradie sa bude rovnať k. Môže nastať iná situácia: medzi maloletými k-tého rádu bude aspoň jeden, ktorý sa nebude rovnať nule, a neplnoletí (k + 1)-ého poradia nemôžu vzniknúť. V tomto prípade sa poradie matice tiež rovná k. stručne povedané, poradie posledného zloženého nenulového vedľajšieho a bude sa rovnať hodnosti matice.
Prejdime na príklady, na ktorých bude proces hľadania hodnosti matice podľa definície názorne znázornený. Ešte raz zdôrazňujem, že v príkladoch k tejto téme nájdeme hodnosť matíc iba pomocou definície hodnosti. Ďalšie metódy (výpočet hodnosti matice metódou ohraničenia maloletých, výpočet hodnosti matice metódou elementárnych transformácií) sú uvedené v nasledujúcich témach.
Mimochodom, nie je vôbec potrebné začať postup na zistenie hodnosti od neplnoletých osôb najmenšieho rádu, ako to bolo urobené v príkladoch č. 1 a č. 2. Okamžite môžete prejsť na maloletých vyšších rádov (pozri príklad č. 3).
Príklad #1
Nájdite poradie matice $A=\left(\begin(pole)(ccccc) 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \koniec(pole)\vpravo)$.
Táto matica má veľkosť $3\krát 5$, t.j. obsahuje tri riadky a päť stĺpcov. Z čísel 3 a 5 je 3 minimum, teda hodnosť matice $A$ je najviac 3, t.j. $\rank A≤ 3 $. A táto nerovnosť je zrejmá, keďže už nemôžeme tvoriť maloletých štvrtého rádu - potrebujú 4 riadky a my máme len 3. Poďme priamo k procesu hľadania hodnosti danej matice.
Medzi neplnoletými prvého rádu (teda medzi prvkami matice $A$) sú nenulové jednotky. Napríklad 5, -3, 2, 7. Vo všeobecnosti nás celkový počet nenulových prvkov nezaujíma. Je tam aspoň jeden nenulový prvok – a to stačí. Keďže medzi maloletými prvého poriadku je aspoň jeden nenulový, usúdime, že $\rang A≥ 1$ a pristúpime k kontrole maloletých druhého poriadku.
Začnime skúmať maloletých druhého rádu. Napríklad na priesečníku riadkov #1, #2 a stĺpcov #1, #4 sú prvky nasledujúceho vedľajšieho: $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end (pole) \vpravo| $. Pre tento determinant sú všetky prvky druhého stĺpca rovné nule, preto samotný determinant je rovný nule, t.j. $\left|\begin(pole)(cc) 5 & 0 \\ 7 & 0 \end(pole) \right|=0$ (pozri vlastnosť #3 vo vlastnosti determinantov). Alebo môžete jednoducho vypočítať tento determinant pomocou vzorca č. 1 z časti o výpočte determinantov druhého a tretieho rádu:
$$ \left|\begin(pole)(cc) 5 & 0 \\ 7 & 0 \end(pole) \right|=5\cdot 0-0\cdot 7=0. $$
Prvý moll druhého rádu, ktorý sme skontrolovali, sa ukázal byť rovný nule. Čo to hovorí? O potrebe ďalšej kontroly maloletých druhého poriadku. Buď sa všetky ukážu ako nula (a potom sa poradie bude rovnať 1), alebo je medzi nimi aspoň jeden neplnoletý, ktorý sa líši od nuly. Pokúsme sa urobiť lepšiu voľbu napísaním druhoradého minor, ktorého prvky sa nachádzajú na priesečníku riadkov #1, #2 a stĺpcov #1 a #5: $\left|\begin(array)(cc) 5 & 2 \\ 7 & 3 \koniec(pole)\vpravo|$. Poďme zistiť hodnotu tohto minoru druhého rádu:
$$ \left|\begin(pole)(cc) 5 & 2 \\ 7 & 3 \end(pole) \right|=5\cdot 3-2\cdot 7=1. $$
Táto vedľajšia hodnota sa nerovná nule. Záver: medzi maloletými druhého rádu je aspoň jeden iný ako nula. Preto $\rank A≥ 2$. Je potrebné pristúpiť k štúdiu maloletých tretieho rádu.
Ak pre tvorbu maloletých tretieho rádu zvolíme stĺpec č. 2 alebo stĺpec č. 4, potom sa takéto maloleté osoby budú rovnať nule (pretože budú obsahovať nulový stĺpec). Zostáva skontrolovať iba jeden malý tretieho rádu, ktorého prvky sa nachádzajú na priesečníku stĺpcov č. 1, č. 3, č. 5 a riadkov č. 1, č. 2, č. 3. Zapíšme si túto drobnosť a nájdime jej hodnotu:
$$ \left|\begin(pole)(ccc) 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end(pole) \right|=-20-18-14 +16+21+15=0. $$
Takže všetci maloletí tretieho rádu sa rovnajú nule. Posledný nenulový moll, ktorý sme zostavili, bol druhého rádu. Záver: maximálne poradie maloletých, medzi ktorými je aspoň jeden iný ako nula, sa rovná 2. Preto $\rang A=2$.
Odpoveď: $\rank A=2$.
Príklad č. 2
Nájdite poradie matice $A=\left(\begin(pole) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0 \\ 9 & 7 & 8 & -7 \end(pole) \vpravo)$.
Máme štvorcovú maticu štvrtého rádu. Hneď si všimneme, že poradie tejto matice nepresahuje 4, t.j. $\rank A≤ 4 $. Začnime hľadať hodnosť matice.
Medzi neplnoletými 1. rádu (teda medzi prvkami matice $A$) je aspoň jeden, ktorý sa nerovná nule, teda $\rang A≥ 1$. Prechádzame k overovaniu maloletých osôb druhého rádu. Napríklad na priesečníku riadkov č. 2, č. 3 a stĺpcov č. 1 a č. 2 dostaneme nasledujúcu moll druhého rádu: $\left| \začiatok(pole) (cc) 4 & -2 \\ -5 & 0 \end(pole) \vpravo|$. Poďme si to spočítať:
$$ \left| \začiatok(pole) (cc) 4 & -2 \\ -5 & 0 \end(pole) \vpravo|=0-10=-10. $$
Medzi maloletými druhého rádu je aspoň jeden, ktorý sa nerovná nule, takže $\rang A≥ 2$.
Prejdime k maloletým tretieho rádu. Nájdime napríklad maloletého, ktorého prvky sa nachádzajú na priesečníku riadkov č. 1, č. 3, č. 4 a stĺpcov č. 1, č. 2, č. 4:
$$ \left | \začiatok(pole) (cccc) -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end(pole) \right|=105-105=0. $$
Keďže sa tento neplnoletý tretí rád rovnal nule, je potrebné vyšetriť ďalšieho maloletého tretieho rádu. Buď sa všetky budú rovnať nule (potom sa poradie bude rovnať 2), alebo medzi nimi bude aspoň jeden, ktorý sa nebude rovnať nule (potom začneme študovať maloletých štvrtého rádu). Uvažujme maloletého tretieho rádu, ktorého prvky sa nachádzajú na priesečníku riadkov č. 2, č. 3, č. 4 a stĺpcov č. 2, č. 3, č. 4:
$$ \left| \začiatok(pole) (ccc) -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end(pole) \right|=-28. $$
Medzi maloletými tretieho rádu je aspoň jeden nenulový neplnoletý, takže $\rang A≥ 3$. Prejdime ku kontrole maloletých štvrtého rádu.
Akákoľvek minorita štvrtého rádu sa nachádza v priesečníku štyroch riadkov a štyroch stĺpcov matice $A$. Inými slovami, minor štvrtého rádu je determinantom matice $A$, pretože táto matica obsahuje iba 4 riadky a 4 stĺpce. Determinant tejto matice bol vypočítaný v príklade č.2 k téme "Zmenšenie poradia determinantu. Rozklad determinantu v riadku (stĺpci)" , zoberme si teda už len hotový výsledok:
$$ \left| \začiatok(pole) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end (pole)\vpravo|=86. $$
Takže, moll štvrtého rádu sa nerovná nule. Už nemôžeme tvoriť maloleté osoby piateho rádu. Záver: najvyššie poradie maloletých, medzi ktorými je aspoň jeden iný ako nula, je 4. Výsledok: $\rang A=4$.
Odpoveď: $\rank A=4$.
Príklad č. 3
Nájdite poradie matice $A=\left(\begin(pole) (cccc) -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end( pole)\right)$.
Hneď si všimnite, že táto matica obsahuje 3 riadky a 4 stĺpce, takže $\rang A≤ 3$. V predchádzajúcich príkladoch sme proces zisťovania hodnosti začali zvažovaním neplnoletých osôb najmenšieho (prvého) rádu. Tu sa pokúsime okamžite skontrolovať maloletých najvyššieho možného poradia. Pre maticu $A$ sú to maloletí tretieho rádu. Uvažujme maloletého tretieho rádu, ktorého prvky ležia na priesečníku riadkov č. 1, č. 2, č. 3 a stĺpcov č. 2, č. 3, č. 4:
$$ \left| \začiatok(pole) (ccc) 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end(pole) \right|=-8-60-20=-88. $$
Takže najvyššie poradie maloletých, medzi ktorými je aspoň jeden, ktorý sa nerovná nule, je 3. Preto je poradie matice 3, t.j. $\poradie A=3$.
Odpoveď: $\rank A=3$.
Vo všeobecnosti je zistenie poradia matice podľa definície vo všeobecnom prípade pomerne časovo náročná úloha. Napríklad relatívne malá matica $5\krát 4$ má 60 maloletých druhého poriadku. A aj keď sa 59 z nich rovná nule, potom sa 60. minor môže ukázať ako nenulový. Potom musíte preskúmať maloletých tretieho rádu, ktorých má táto matica 40 kusov. Zvyčajne sa snaží použiť menej ťažkopádne metódy, ako je metóda ohraničenia maloletých alebo metóda ekvivalentných transformácií.
§3. Hodnosť matice
Určenie hodnosti matice
Lineárne závislé riadky
Transformácie elementárnej matice
Ekvivalentné matice
Algoritmus na zistenie hodnosti matice pomocou elementárnych transformácií
§štyri. Determinanty prvého, druhého a tretieho rádu
Determinant prvého rádu
Determinant druhého rádu
Determinant tretieho rádu
Sarrus vládne
§5. Výpočet determinantov veľkých zákaziek
Algebraické sčítanie
Laplaceova veta
Determinant trojuholníkovej matice
Aplikácia. Pojem determinantu P poradie vo všeobecnosti.
§ 3. Hodnosť matice
Každá matica je charakterizovaná určitým číslom, ktoré je dôležité pri riešení systémov lineárnych rovníc. Toto číslo sa volá maticová hodnosť.
Hodnosť matice sa rovná počtu jeho lineárne nezávislých riadkov (stĺpcov), cez ktoré sú lineárne vyjadrené všetky jeho ostatné riadky (stĺpce).
Riadky (stĺpce) matice sa nazývajú lineárne závislé ak sú ich zodpovedajúce prvky proporcionálne.
Inými slovami, prvky jedného z lineárne závislých riadkov sa rovnajú prvkom druhého, vynásobené rovnakým číslom. Napríklad riadky 1 a 2 matice ALE sú lineárne závislé, ak , kde (λ je nejaké číslo).
Príklad. Nájdite hodnosť matice
Riešenie.
Druhý riadok sa získa z prvého, ak sa jeho prvky vynásobia -3, tretí sa získa z prvého, ak sa jeho prvky vynásobia 0, a štvrtý riadok nemožno vyjadriť ako prvý. Ukazuje sa, že matica má dva lineárne nezávislé riadky, pretože prvý a štvrtý riadok nie sú proporcionálne, preto je poradie matice 2.
Hodnosť matice ALE označené hodnosť A alebo r(A).
Z definície hodnosti matice vyplýva:
1. Hodnosť matice nepresahuje najmenší z jej rozmerov, t.j. pre maticu A m × n .
2. Hodnosť matice je nulová, iba ak ide o nulovú maticu.
Vo všeobecnom prípade je určenie hodnosti matice dosť namáhavé. Na uľahčenie tejto úlohy sa používajú transformácie, ktoré zachovávajú hodnosť matice, ktoré sú tzv elementárne transformácie:
1) vyradenie nulového riadku (stĺpca);
2) násobenie všetkých prvkov riadku (stĺpca) číslom iným ako nula;
3) zmena poradia riadkov (stĺpcov);
4) pridanie k prvkom jedného riadka (stĺpca) zodpovedajúcich prvkov iného riadku (stĺpca), vynásobené ľubovoľným číslom;
5) maticová transpozícia.
Dve matice sa nazývajú ekvivalent ak sa jedno získa od druhého konečným počtom elementárnych transformácií.
Ekvivalencia matíc je označená znakom "~" (ekvivalent).
Pomocou elementárnych transformácií je možné akúkoľvek maticu zredukovať na trojuholníkový tvar, potom výpočet jej poradia nie je náročný.
Proces výpočtu hodnosti matice pomocou elementárnych transformácií pozrime sa na príklad.
Príklad. Nájdite hodnosť matice
A = 
Riešenie.
Našou úlohou je uviesť matricu do trojuholníkového tvaru, t.j. pomocou elementárnych transformácií zabezpečte, aby pod hlavnou uhlopriečkou v matici boli iba nuly.
1. Zvážte prvý riadok. Ak prvok a 11 = 0, potom pri permutácii riadkov alebo stĺpcov to dosiahneme a 11 ¹ 0. V našom príklade si vymeníme napríklad prvý a druhý riadok matice:
A = 
Teraz prvok a 11 ¹ 0. Vynásobením prvého riadku vhodnými číslami a sčítaním s ďalšími riadkami zabezpečíme, že všetky prvky prvého stĺpca (okrem a 11) boli rovné nule.
2. Zvážte teraz druhý riadok. Ak prvok a 22 = 0, potom pri permutácii riadkov alebo stĺpcov to dosiahneme a 22 ¹ 0. Ak prvok a 22 ¹ 0 (a máme a 22 = –1 ¹ 0), potom vynásobením druhého riadku vhodnými číslami a pridaním do ďalších riadkov zabezpečíme, že všetky prvky druhého stĺpca (okrem a 22) boli rovné nule.
3. Ak sa v procese transformácií získajú riadky (stĺpce), ktoré pozostávajú výlučne z núl, potom ich zahodíme. V našom príklade zahodíme riadky 3 a 4:
Posledná matica má stupňovitý tvar a obsahuje dva riadky. Sú lineárne nezávislé, preto je poradie matice 2.
§ štyri. Determinanty prvého, druhého a tretieho rádu
Spomedzi rôznych matíc sú štvorcové matice oddelené. Tento typ matice je dobrý, pretože:
1. Identitné matice sú štvorcové.
2. Môžete násobiť a sčítať ľubovoľné štvorcové matice rovnakého rádu a dostanete maticu rovnakého rádu.
3. Štvorcové matice môžu byť umocnené.
Tiež iba štvorcové matice môžu mať determinant.
Maticový determinant je špeciálne číslo vypočítané podľa nejakého pravidla. Maticový determinant ALE označené:
Alebo s rovnými zátvorkami: ,
Alebo veľké grécke písmeno "delta": Δ( A),
Alebo symbol "determinant": det ( A).
Determinant matice prvého rádu ALE= (a 11) alebo determinant prvého rádu, je číslo rovné prvku matice:
∆1 = 
=a 11
Maticový determinant druhého rádu 
alebo determinant druhého rádu
Príklad:
Determinant matice tretieho rádu 
alebo determinant tretieho rádu, je číslo, ktoré sa vypočíta podľa vzorca:
Determinant tretieho rádu možno vypočítať pomocou Sarrus vládne .
Sarrus vládne. Prvé dva stĺpce sú podpísané na determinante tretieho rádu vpravo a so znamienkom plus (+) berú súčet súčinov troch prvkov umiestnených na hlavnej diagonále determinantu a na "priamkach" rovnobežných s hlavná uhlopriečka, so znamienkom mínus (-) berú súčet súčinov prvkov umiestnených na druhej uhlopriečke a na "priamkych" rovnobežných s ňou.
Príklad:
Je ľahké vidieť, že počet členov v determinante rastie s jeho poradím. Vo všeobecnosti v determinante P rádu, počet termínov je 1 2 3 ... P = P!.
Skontrolujeme: pre Δ 1 je počet členov rovný 1! = 1,
pre Δ 2 je počet členov 2! = 1 2 = 2,
pre Δ 3 je počet členov 3! = 1 2 3 = 6.
Z toho vyplýva, že pre determinant 4. rádu je počet členov 4! = 1 2 3 4 = 24, čo znamená, že výpočet takéhoto determinantu je dosť prácny, nehovoriac o determinantoch vyššieho rádu. Vzhľadom na to sa snažia zredukovať výpočet determinantov veľkých rádov na výpočet determinantov druhého alebo tretieho rádu.
§ 5. Výpočet determinantov veľkých zákaziek
Predstavme si niekoľko pojmov.
Nech je daná štvorcová matica A n- poradie:
| A= |  |
Menší M ij prvok a ij sa nazýva determinant ( P– 1. rád získaný z matice ALE vyškrtnúť i-tý riadok a j-tý stĺpec.
Napríklad moll prvku a 12 matíc tretieho rádu bude:
Algebraické sčítanie ALE ij prvok a ij je jeho moll, braný so znamienkom (−1) i + j:
ALE ij = (-1) i + j M ij
Inými slovami, ALE ij = M ij ak i+j párne číslo,
ALE ij = - M ij ak i+j nepárne číslo.
Príklad. Nájdite algebraické doplnky prvkov druhého riadku matice
Riešenie.
Pomocou algebraických doplnkov je možné vypočítať determinanty veľkých rádov na základe Laplaceovej vety.
Laplaceova veta. Determinant štvorcovej matice sa rovná súčtu súčinov prvkov ktoréhokoľvek z jej riadkov (stĺpcov) a ich algebraických doplnkov:
– rozklad na i-tom riadku;
( je expanzia v j-tom stĺpci).
Príklad. Vypočítajte determinant matice 
rozklad na prvom riadku.
Riešenie.
Takže determinant akéhokoľvek rádu môže byť redukovaný na výpočet niekoľkých determinantov menšieho rádu. Je zrejmé, že pre rozšírenie je vhodné zvoliť riadok alebo stĺpec obsahujúci čo najviac núl.
Uvažujme ešte o jednom príklade.
Príklad. Vypočítajte determinant trojuholníkovej matice 
Riešenie.
Mám to determinant trojuholníkovej matice sa rovná súčinu prvkov jej hlavnej uhlopriečky .
Tento dôležitý záver uľahčuje výpočet determinantu akejkoľvek trojuholníkovej matice. Je to o to užitočnejšie, že v prípade potreby možno akýkoľvek determinant zredukovať na trojuholníkový tvar. V tomto prípade sa používajú niektoré vlastnosti determinantov.
Aplikácia
Pojem determinantu P poradie vo všeobecnosti.
Vo všeobecnosti je možné definovať maticový determinant presne P rádu, ale na to je potrebné zaviesť niekoľko pojmov.
permutáciačísla 1, 2, ..., n nazýva sa akékoľvek usporiadanie týchto čísel v určitom poradí. V elementárnej algebre je dokázané, že počet všetkých permutácií, z ktorých možno vytvoriť nčísla je 12...n = n!. Napríklad tri čísla 1, 2, 3 môžu tvoriť 3! = 6 permutácií: 123, 132, 312, 321, 231, 213.
Hovoria, že v danej permutácii čísla i a j tvoria inverzia(porucha) ak i> j, ale i stojí v tejto permutácii predtým j, teda ak je väčšie číslo vľavo od menšieho.
Permutácia je tzv dokonca(alebo zvláštny) ak je celkový počet prevrátení párny (nepárny), resp.
Operácia, pomocou ktorej sa prechádza z jednej permutácie do druhej, zloženej z toho istého nčísla sa volá substitúcia n stupeň.
Substitúcia, ktorá transformuje jednu permutáciu na inú, sa zapíše do dvoch riadkov v spoločných zátvorkách a čísla, ktoré v uvažovaných permutáciách zaberajú rovnaké miesta, sa nazývajú zodpovedajúce a zapisujú sa pod seba. Napríklad symbol
označuje permutáciu, v ktorej 3 prechádza na 4, 1 na 2, 2 na 1, 4 na 3. Permutácia sa nazýva párna (alebo nepárna), ak je celkový počet inverzií v oboch radoch substitúcie párny (nepárny). Akákoľvek náhrada n stupeň možno písať ako
tie. s prirodzeným usporiadaním čísel v hornom riadku.
Dostaneme štvorcovú maticu poriadku n
Zvážte všetky možné produkty n prvky tejto matice, prevzaté po jednom z každého riadku a každého stĺpca, t.j. diela vo forme:
,
kde indexy q 1 , q 2 ,..., q n vytvoriť nejakú permutáciu čísel
1, 2,..., n. Počet takýchto produktov sa rovná počtu rôznych permutácií z n znaky, t.j. rovná sa n!. Pracovné znamenie , rovná sa (–1) q, kde q je počet inverzií v permutácii druhých indexov prvkov.
determinant n- poradie sa nazýva algebraický súčet všetkých možných súčinov nad n prvky matice, prevzaté len jeden z každého riadku a každého stĺpca, t.j. diela vo forme: . Zároveň znakom diela rovná sa (-1) q, kde q je počet inverzií v permutácii druhých indexov prvkov.
Lineárna algebra
Zvážte pravouhlú maticu. Ak v tejto matici vyberáme ľubovoľne k linky a k stĺpce, potom prvky v priesečníku vybraných riadkov a stĺpcov tvoria štvorcovú maticu k-tého rádu. Determinant tejto matice je tzv k-teho rádu menšieho matica A. Je zrejmé, že matica A má vedľajšie čísla ľubovoľného rádu od 1 po najmenšie z čísel m a n. Medzi všetkými nenulovými neplnoletými matice A je aspoň jeden neplnoletý, ktorého poradie je najväčšie. Najväčšie z nenulových rádov neplnoletých v danej matici sa nazýva hodnosť matice. Ak je poradie matice A r, potom to znamená, že matica A má nenulový menší rád r, ale každý menší rád väčší ako r, rovná sa nule. Hodnosť matice A je označená r(A). Je zrejmé, že vzťah
Výpočet hodnosti matice pomocou maloletých
Hodnosť matice sa zistí buď ohraničením neplnoletých osôb, alebo metódou elementárnych transformácií. Pri výpočte hodnosti matice prvým spôsobom by sa malo prejsť od neplnoletých nižších rádov k maloletým vyššieho rádu. Ak už bol nájdený nenulový vedľajší D k-teho rádu matice A, tak treba vypočítať len (k + 1)-ého rádu vedľajších hraničiacich s vedľajším D, t.j. ktorý ho obsahuje ako maloletú. Ak sú všetky nulové, potom je poradie matice rovnaké k.
Príklad 1Nájdite hodnosť matice metódou ohraničenia maloletých
.
Riešenie.Začíname maloletými 1. rádu, t.j. z prvkov matice A. Vyberme si napríklad vedľajší (prvok) М 1 = 1 nachádzajúci sa v prvom riadku a prvom stĺpci. Ohraničením pomocou druhého riadku a tretieho stĺpca získame vedľajšiu M 2 = , ktorá je odlišná od nuly. Teraz sa obrátime na maloletých 3. rádu, hraničiacich s M 2 . Sú len dva (môžete pridať druhý stĺpec alebo štvrtý). Vypočítame ich: 
=
0. Ukázalo sa teda, že všetci hraničiaci maloletí tretieho rádu sa rovnajú nule. Hodnosť matice A je dva.
Výpočet hodnosti matice pomocou elementárnych transformácií
ZákladnéNasledujúce maticové transformácie sa nazývajú:
1) permutácia akýchkoľvek dvoch riadkov (alebo stĺpcov),
2) vynásobením riadka (alebo stĺpca) nenulovým číslom,
3) pridanie do jedného riadka (alebo stĺpca) ďalšieho riadka (alebo stĺpca) vynásobeného nejakým číslom.
Dve matice sa nazývajú ekvivalent, ak jeden z nich získame od druhého pomocou konečnej množiny elementárnych transformácií.
Ekvivalentné matice nie sú vo všeobecnosti rovnaké, ale ich poradie je rovnaké. Ak sú matice A a B ekvivalentné, potom sa to zapíše takto: A~b.
Kanonickýmatica je matica, ktorá má niekoľko 1 v rade na začiatku hlavnej uhlopriečky (ktorej počet môže byť nula) a všetky ostatné prvky sa rovnajú nule, napr.
.
Pomocou elementárnych transformácií riadkov a stĺpcov možno ľubovoľnú maticu zredukovať na kanonickú. Hodnosť kanonickej matice sa rovná počtu jednotiek na jej hlavnej uhlopriečke.
Príklad 2Nájdite hodnosť matice
a priviesť ho do kánonickej podoby.
Riešenie. Odčítajte prvý riadok od druhého a usporiadajte tieto riadky:
.
Teraz od druhého a tretieho riadku odpočítajte prvý vynásobený 2 a 5:
;
odpočítať prvý od tretieho riadku; dostaneme maticu
ktorá je ekvivalentná matici A, keďže sa z nej získava pomocou konečnej množiny elementárnych transformácií. Je zrejmé, že poradie matice B je 2, a teda r(A)=2. Maticu B možno ľahko zredukovať na kanonickú. Odčítaním prvého stĺpca vynásobeného vhodnými číslami od všetkých nasledujúcich vynulujeme všetky prvky prvého riadku okrem prvého a prvky zostávajúcich riadkov sa nemenia. Potom odčítaním druhého stĺpca, vynásobeného príslušnými číslami, od všetkých nasledujúcich, vynulujeme všetky prvky druhého riadku, okrem druhého, a získame kanonickú maticu:
.
Riadky (stĺpce). Niekoľko riadkov (stĺpcov) sa nazýva lineárne nezávislých, ak žiadny z nich nemožno lineárne vyjadriť inými. Hodnosť systému riadkov sa vždy rovná hodnote systému stĺpcov a toto číslo sa nazýva poradie matice.
Hodnosť matice je najvyššia zo všetkých možných nenulových neplnoletých osôb tejto matice. Hodnosť nulovej matice akejkoľvek veľkosti je nula. Ak sa všetci maloletí druhého poriadku rovnajú nule, potom sa hodnosť rovná jednej atď.
Matrix rank - rozmer obrazu dim (im (A)) (\displaystyle \dim(\operatorname (im) (A))) lineárny operátor , ktorý zodpovedá matici.
Zvyčajne hodnosť matice A (\displaystyle A) označené poradie A (\displaystyle \operatorname (rang) A), r A (\displaystyle \operatorname (r) A), rg A (\displaystyle \operatorname (rg) A) alebo hodnotenie A (\displaystyle \operatorname (rank) A). Posledná možnosť je typická pre angličtinu, zatiaľ čo prvé dve sú pre nemčinu, francúzštinu a množstvo ďalších jazykov.
Encyklopedický YouTube
-
1 / 5
Nech je obdĺžniková matica.
Potom, podľa definície, hodnosť matice A (\displaystyle A) je:
Veta (o správnosti definície hodností). Nech sú všetci matice maloletí A m × n (\displaystyle A_(m\times n)) objednať k (\displaystyle k) sa rovnajú nule ( M k = 0 (\displaystyle M_(k)=0)). Potom ∀ M k + 1 = 0 (\displaystyle \forall M_(k+1)=0) ak existujú.
Súvisiace definície
Vlastnosti
- Veta (na základe vedľajšej): Nechaj r = zvonenie A , M r (\displaystyle r=\meno operátora (rang) A,M_(r))- menší základ matice A (\displaystyle A), potom:
- Dôsledky:
- Veta (o invariancii poradia pri elementárnych transformáciách): Zaveďme si zápis matíc získaných od seba elementárnymi transformáciami . Potom je pravdivé tvrdenie: Ak A ∼ B (\displaystyle A\sim B), potom sú ich rady rovnaké.
- Veta Kronecker - Cappelli: Systém lineárnych algebraických rovníc je konzistentný vtedy a len vtedy, ak sa hodnosť jeho hlavnej matice rovná hodnote jeho rozšírenej matice. Konkrétne:
- Počet hlavných premenných systému sa rovná hodnosti systému.
- Konzistentný systém bude definovaný (jeho riešenie je jedinečné), ak sa hodnosť systému rovná počtu všetkých jeho premenných.
- Nerovnosť Sylvester: Ak A a B veľkostné matice m x n a n x k, potom
Toto je špeciálny prípad nasledujúcej nerovnosti.
- Nerovnosť Frobenius: Ak sú AB, BC, ABC dobre definované, potom
Lineárna transformácia a poradie matice
Nechaj A (\displaystyle A)- matica veľkosti m × n (\displaystyle m\times n) nad ihriskom C (\displaystyle C)(alebo R (\displaystyle R)). Nechaj T (\displaystyle T) je lineárna transformácia zodpovedajúca A (\displaystyle A) v štandardnom základe; znamená to, že T (x) = A x (\displaystyle T(x)=Ax). Hodnosť matice A (\displaystyle A) je rozmer rozsahu transformácie T (\displaystyle T).
Metódy
Existuje niekoľko metód na zistenie poradia matice:
- Metóda elementárnych transformácií
- Metóda Fringing Minor